Olimpiai szakkörök 2005-ben:

január 14, 28, február 11, 25, március 11, április 1, 15, 29, május 13.

2005. január 14.

1. Az ABC háromszög köré írt körének pontja P. P merőleges vetülete az oldalegyenesekre A’, B’, C’. Igazoljuk, hogy A’, B’, C’ egy egyenesen vannak.

2. Vannak-e olyan a, b, c, d, x egészek, amelyekre .

3. Egy ötszög csúcsaira valós számokat írtunk. A csúcsokat összekötő szakaszokra ráírtuk a végpontokon levő két szám összegét. Ez utóbbi számok közül 7-ről tudjuk, hogy egész. Igazoljuk, hogy a többi is az.

4. Az ABC háromszög magasságpontja M, körülírt körének középpontja O, sugara R. Tükrözzük a háromszög csúcsait rendre a szemközti oldalegyenesekre; legyenek a tükörképek X,Y,Z, és tegyük fel, hogy ezek a tükörképek egy egyenesen vannak.

Mutassuk meg, hogy OM = 2R.

5. Okos Ottó felsorolta az n természetes szám pozitív osztóit nagyság szerinti sorrendben. Elsőként az 1-et, majd sorban egymás után, végül nyolcadikként következett az n. A hatodikként felsorolt d osztóról tudjuk, hogy 19<d<26. Mi lehetett n?

6. Az ABCD trapézban a párhuzamos oldalak AB és CD, AC=BC. Az AB oldal felezőpontja F, az F-et tartalmazó e egyenes az AD szárat P-ben, a BD átló B-n túli meghosszabbítását pedig Q-ban metszi. Legyen . Mekkora a szög?

Házi feladat: 7. Egy sakk körmérkőzésnek k résztvevője volt (k páratlan); mindenki mindenkivel pontosan egyszer játszott; győzelemért 2, döntetlenért 1, vereségért 0 pontot kaptak. A verseny végén mindenkinek más volt az elért pontszáma. Legfeljebb mennyi lehetett a döntetlen játékok száma?

2005. január 28.

1. Az M halmaz elemei egészek. Az elemeket csökkenő sorrendben váltakozó előjellel összeadva kapjuk az S(M) értéket. Pl S({1, 2, 5, 8})=8–5+2–1=4 Mennyi lesz az S(M) értékek összege, ha M végigfut az {1, 2, …, 7} halmaz összes részhalmazán?

2. Adott 2005 halmaz, mindegyik 45 elemű. Bármely kettőnek pont 1 közös eleme van. Bizonyítsuk be, hogy mindnek egy közös eleme van.

3. A H={1, 2, …, 20) halmaz 9 elemű részhalmazaihoz az f függvény hozzárendel egy számot H-ból. Igazoljuk, hogy H-nak van olyan tízelemű T részhalmaza, melyre f(T\{k})¹k teljesül, ha k eleme T-nek.

4. Egy vállalatnak 70 dolgozója van. Bármely két dolgozó –A és B– esetén van olyan nyelv, melyet A beszél, de B nem és van olyan nyelv, melyet B beszél, de A nem. Legalább hány nyelvet beszélnek a vállalat dolgozói?

Ezen feladat kapcsán kimondtuk és bizonyítottuk Sperner tételét: Egy n elemű halmaznak legfeljebb részhalmaza adható meg úgy, hogy semelyik se tartalmazza valamely másikat.

5. Egy konferencián 9 tudós vett részt. Bármelyikük legfeljebb 3 nyelven beszélt. Bármely három közt van kettő olyan, akik beszélnek közös nyelvet. Igazoljuk, hogy létezik olyan nyelv, melyen legalább hárman beszélnek.

6. Egy 100 elemű halmaznak legfeljebb hány részhalmaza adható meg úgy, hogy közülük bármely kettő vagy diszjunkt, vagy az egyik tartalmazza a másikat.

Házi feladat 7. Bergengócia egy városában 2004-en laknak. 3 fős klubokat alakítanak, összesen 2005-öt. Bármely két klub tagsága legalább egy emberben különbözik. Igazoljuk, hogy létezik két olyan klub, melyeknek pont 1 közös tagja van.

2005. február 11.

1. Az ABC háromszög minden csúcsa az N négyzet belsejében van. A csúcsok tükörképei a háromszög súlypontjára A’, B’, C’. Igaz-e, hogy ezek közül legalább egy N-nek belső pontja?

2. Az ABC háromszög B illetve C csúcsából induló szögfelezőinek talppontja M illetve N. Az M kezdőpontú MN félegyenes a köréírt kört D-ben metszi. Bizonyítsuk be, hogy .

3. Az ABC háromszög magasságpontján áthalad az e egyenes. Igazoljuk, hogy e-nek az oldalegyenesekre való tükörképei egy ponton haladnak át.

A feladat több következményét is tárgyaltuk. (1.) Parabola három érintője alkotta háromszög magasságpontján áthalad a vezéregyenes. (2.) Tetszőleges f egyenest az ABC háromszög oldalegyeneseire tükrözve a kapott egyenesek alkotta háromszög beírt körének középpontja az ABC köréírt körén van. (3.) Négy egyenes által alkotott háromszögek köréírt körei egy ponton haladnak át. Ez a pont a fókusza annak a parabolának, melynek az adott egyenesek érintői, vezéregyenese az érintők által alkotott háromszögek magasságpontjai által meghatározott egyenes.

4. Az ABC háromszög beírt köre az AB, AC, BC oldalakat rendre K, M, N pontokban érinti. AC felezőpontja F. BF és MN metszéspontja T. Igazoljuk, hogy TK merőleges AC-re.

Házi feladat: 5. Igazoljuk, hogy egy háromszög Euler egyenese akkor és csak akkor párhuzamos BC-vel, ha .

2005. február 25.

1. A 93-as diákolimpia 3. feladata. Egy végtelen sakktábla egy n-szer n-es négyzetében minden mezőn áll egy figura. Egy lépésben egy figura átugorhat egy élszomszédos mezőn álló figurát, ha üres mezőre érkezik az ugrás, s az átugrott figurát levesszük a tábláról. Mely n-re érhető el, hogy csak egy figura maradjon néhány lépés után?

2. A 92-es diákolimpia 3. feladata. Egy 9 pontú gráf élei közül néhányat pirosra, néhányat kékre festettek. Mi a legkisebb n, melyre n színezett él esetén biztosan lesz piros, vagy kék háromszög a gráfban.

3. A 93-as diákolimpia 1. feladata. Legyen f(x)=xⁿ+5x^n-1+3, ahol n legalább 2 és egész. Bizonyítsuk, hogy f(x) nem írható fel két legalább elsőfokú egész együtthatós polinom szorzataként.

Házi feladat: 4. A 91-es diákolimpia 5. feladata. Legyen P az ABC háromszög belső pontja. Igazoljuk hogy a PAB, PBC, PCA szögek közül legalább az egyik nem nagyobb 30˚-nál.

2005. március 11.

Megbeszéltük a válogatóverseny feladatait, megoldásait. Ezek a következők voltak:

1. Bergengóciában 2005 város van. Fejletlen a csőpostahálózat; semely két várost nem köti össze közvetlen cső. Az új szabályok értelmében kiépíthetnek közvetlen csőkapcsolatot az A és B város között, ha létezik még két további város C és D úgy, hogy nincs közvetlen csőposta sem A és C, sem C és D, sem D és B között.

Legfeljebb hány csövet építhetnek ki?

2. A k kör és az l egyenes nem metszik egymást. A kör AB átmérője l-re merőleges, az átmérő végpontjai közül B van közelebb l-hez. A kör A-tól és B-től különböző pontja C. Az AC egyenes és l metszéspontja D. D-ből érintőt húzunk a körhöz, az érintési pont E. Tudjuk, hogy B és E az AC egyenesnek ugyanazon oldalán vannak. A BE egyenes és l metszéspontja F. Az AF egyenes a kört G-ben metszi. Igazoljuk, hogy az AB egyenesre tükrözve G-t a CF egyenes egy pontját kapjuk.

3. Legyen p egy 2-nél nagyobb prím. A pozitív egészek a₁, a₂, …, a_p-2 sorozatáról tudjuk, hogy p nem osztja sem a_k-t, sem (a_k^k–1)-et (k=1,2, …, p–2). Igazoljuk, hogy a sorozat néhány tagjának szorzata 2 maradékot ad p-vel osztva.

A házi feladat kapcsán felelevenítettük az Erdős-Mordell egyenlőtlenséget.

4. Ha a PAB, PBC, PCA szögek egyenlők, akkor P a háromszög Brocard pontja. Igazoljuk, hogy az említett szög cotangense egyenlő a háromszög szögei kotangenseinek összegével:

.

5. Igazoljuk, hogy egy háromszög szögeire teljesül:

.

A 4. és 5. feladat segítségével új bizonyítást adtunk a legutóbbi szakkör 4. feladatára.

2005. április 1.

Ezt a szakkört Hraskó András tanár úr vezette, az itt következő anyagot is ő írta le:

1. feladat

Alapkonfiguráció: Az adott r sugarú k_A, k_B körök.

Kezdőpont: A k_A kör olyan A₀ pontja, amelyhez van a K_B körön olyan B₀ pont, amelyre A₀B₀ = r.

Pontsorozat: Olyan A₀B₀A₁B₁A₂B₂... pontsorozat, amelynek tagjai felváltva k_A-ra illetve K_B-re illeszkednek, az egymást követő pontok közti távolság pedig mindig r. A sorozat másodszomszédos elemei (A_i és A_i+1, illetve B_i és B_{i +1}) lehetőleg különbözők.

Állítás: A pontsorozat periodikus. Milyen hosszú a periódus?

2. feladat

Határozzuk meg a 2, 3, 4, … ,102  számok mindazon  a₁, a₂, … , a₁₀₁ sorba-rendezéseinek számát,  melyekre minden k esetén a_k osztható k-val!

Városok Viadala 1980, Junior 3. példa

3. feladat

Bizonyítsuk be, hogy bármely háromszög belső szögeire teljesül az

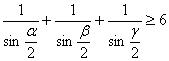
egyenlőtlenség!

4. feladat

Ismeretes, hogy ha egy 36°-os szög csúcsából elindulunk és a szárak között egy rögzített távolsággal ugrálunk, akkor öt lépés után visszajutunk a szög csúcsába.

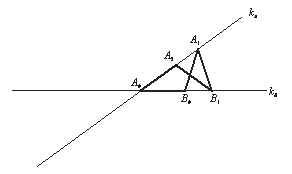
Mi történik akkor, ha nem a szög csúcsából indulunk ki?

5. feladat

Határozzuk meg az összes olyan, nem azonosan nulla P(x) polinomot, amelyre

a) P(x²) º (P(x))²;

b) P(x²- 2x) º (P(x-2))²;

6. feladat

Oldja meg az x⁶ + x³y = y³ + 2y² egyenletet az egész szám(pár)ok körében!

Házi feladatok

1. Egy négyszög csúcsai az R sugarú k körön, oldalfelező pontjai pedig az r sugarú l körön vannak. Jelölje d a két kör középpontjának távolságát.

a) Milyen algebrai összefüggést elégítenek ki az R, r, d mennyiségek?

b) Mutassuk meg, hogy ha A₀A₁ a k olyan húrja, amelynek felezőpontja l-en van, akkor befejezhető olyan (esetleg hurkolt) négyszöggé, amelynek csúcsai k-ra, oldalfelezőpontjai pedig l-re illeszkednek!

2. Oldja meg az x(x+1)(x+7)(x+8) = y² egyenletet az egész szám(pár)ok körében!

3. Mutassuk meg, hogy a hegyesszögű háromszög beírt (r) és körülírt (R) körének sugara és magasságai között fennáll a

9r £ m_a + m_b + m_c £ 9R/2

egyenlőtlenség!

Segítség: Kubatov Antal interneten olvasható cikkében.

4.* Határozzuk meg az összes olyan valós együtthatós P(x) polinomot, amely teljesíti a

P(x)P(2x²) º P (2x² + x)

azonosságot!

Megoldások, útmutatás:

Olimpiai szakkör

2005. április 1.

A feladatok megoldásai

1. feladat

Alapkonfiguráció: Az adott r sugarú k_A, k_B körök.

Kezdőpont: A k_A kör olyan A₀ pontja, amelyhez van a K_B körön olyan B₀ pont, amelyre A₀B₀ = r.

Pontsorozat: Olyan A₀B₀A₁B₁A₂B₂... pontsorozat, amelynek tagjai felváltva k_A-ra illetve K_B-re illeszkednek, az egymást követő pontok közti távolság pedig mindig r. A sorozat másodszomszédos elemei (A_i és A_i+1, illetve B_i és B_{i +1}) lehetőleg különbözők.

Állítás: A pontsorozat periodikus. Milyen hosszú a periódus?

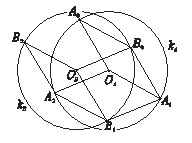Megoldás

Az ábrán a k_A, k_B körök helyett csak azok O_A, O_B középpontjait és a belőlük a poligon csúcsaiba futó sugarakat jelöltük. Az ábrán jelölt szakaszok mind r hosszúságúak és azt kell bebizonyítani, hogy B₃A₁ hossza is éppen r.

Az A₀B₀, O_AA₁, A₂B₁, B₂O_B szakaszok párhuzamosak egymással, hiszen az A₀B₀A₁O_A, O_AA₁B₁A₂, A₂B₁O_BB₂ négyszögek mind rombuszok. Így az A₀B₀O_BB₂ négyszög is paralelogramma, tehát A₀B₂ a vele szemközti B₀O_B szakasszal együtt r hosszúságú.

Az ábrán egy kocka élhálóját láthatjuk. Sok más elemi geometriai feladat is ugyanerre a konfigurációra vezet vissza (lásd pld. az alábbi példákat).

1.1 Adott három egyenlő (r) sugarú K₁, K₂, K₃ kör, melyek mind átmennek egy P ponton. A körök további három pontban metszik egymást. Ezek rendre Q₁₂, Q₂₃ és Q₃₁.

a) Bizonyítsd be, hogy a Q₁₂Q₂₃Q₃₁ háromszög magasságpontja a P pont!

b) Bizonyítsd be, hogy a Q₁₂Q₂₃Q₃₁ háromszög köréírt köre r sugarú!

1.2 A, B és C egy r sugarú kör három olyan különböző pontja, hogy nincs közöttük átellenes. Rajzoljunk az AB, BC és CA szakaszokra, mint alapokra ABC', BCA' és CAB' egyenlő szárú háromszögeket úgy, hogy száraik hossza r legyen, és az A', B', C' pontok különbözzenek a kör középpontjától!

Igazoljuk, hogy az A'B'C' háromszög egybevágó az ABC háromszöggel!

2. feladat

Határozzuk meg a 2, 3, 4, … ,102  számok mindazon  a₁, a₂, … , a₁₀₁ sorba-rendezéseinek számát,  melyekre minden k esetén a_k osztható k-val!

Városok Viadala 1980, Junior 3. példa

Állítás

Ha k nem osztja 102-t, akkor a_k = k.

Bizonyítás

Fordított indukciót alkalmazunk. A legnagyobb szóbajövő szám a 101.

101½a₁₀₁ nyilván csak úgy lehetséges, hogy ha a₁₀₁ = 101. Tegyük most fel, hogy

az állítás igaz minden n < k számra és n nem osztja 102-t. n½a_n, így a_n vagy n vagy n valamely többese, de n többesei sem osztói 102-nek és nagyobbak, mint n, így azokra k=a_k. Ezért a_n-re csak n marad. Ezzel az állítást igazoltuk.

Tehát csak 102 osztóival kell foglalkozni. Itt azért van lehetőség némi „játék”-ra, mert az 1 számot nem kell beírni a sorozatba, és nincs a₁₀₂.

I. megoldás

Tegyük fel, hogy a_d = 102. Ekkor d½102. Ha k nem osztja d-t, akkor a fenti módon igazolható, hogy a_k = k. Így az ilyen megoldások száma, annyi ahány megoldás lenne az eredeti feladatra 102 helyett d-vel, illetve a d = 1 eset egy megoldást jelent.

Tehát, ha f(n) jelöli a 2, 3, ..., n számok olyan a₁, a₂, ..., a_n-1 sorbarendezéseinek számát, amelyre kÎ{1, 2, ..., n-1} esetén kïa_k, akkor f(1) = 1 mellett

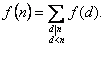
Speciálisan f(prím) = 1.

f(102) = f(1) + f(2) + f(3) + f(17) + f(6) + f(34) + f(51), ahol f(1) = f(2) = f(3) = f(17) = 1,

f(6) = f(1) + f(2) + f(3) = 1 + 1 + 1 = 3, és ugyanígy f(34) = f(51) = 3, tehát f(102) = 13.

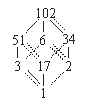
II. megoldás

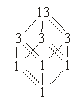Rajzoljuk le 102 osztóinak rendszerét, azaz 102 osztóhálóját! Az osztók közül ki kell venni az 1-et, helyét valamely másik osztóval betölteni, annak helyét is betölteni stb., míg végül a 102 is lejjebb kerül. Tehát végül is az 1-ből a 102-be vezető utak számát kell összeszámolni (a Pascal háromszöghöz némiképp hasonlóan) csak most nem kell feltétlenül az éleken haladni, hanem több lépést összevonhatunk, ugorhatunk. Ilyen utak pld:

1®102, 1®2®102 vagy 1®2®6®102.

Egy adott csúcsba vezető utak száma most az összes alatta lévő csúcsokba vezető utak számának összege (lásd az ábrát). Tehát összesen 13 megoldás van.

Probléma

A szakkörvezető sem tud explicit képletet a megoldásra. Még f(p^a×q^b) explicit előállítását is szívesen fogadja (p és q különböző prímek).

3. feladat

Bizonyítsuk be, hogy bármely háromszög belső szögeire teljesül az

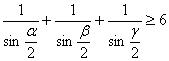
egyenlőtlenség!

I. megoldás: Alkalmazzuk az Erdős-Mordell tételt a háromszög beírt körének középpontjára!

A feladat Kubatov Antal cikkéből származik.

II. megoldás

Alkalmazzuk a harmonikus és a számtani közép közti egyenlőtlenséget, majd a Jensen egyenlőtlenséget!

4. feladat

Ismeretes, hogy ha egy 36°-os szög csúcsából elindulunk és a szárak között egy rögzített távolsággal ugrálunk, akkor öt lépés után visszajutunk a szög csúcsába.

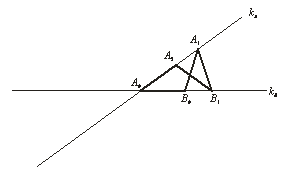
Mi történik akkor, ha nem a szög csúcsából indulunk ki?

Állítás: mindig 10 lépésben jutunk vissza.

I. megoldás ötlete (Paulin Roland)

Keressük meg a szabályos ötszöget a feladatban!

II. megoldás ötlete (Kiss Gergő)

Keressünk olyan mennyiséget, amely minden lépésben ugyanannyival nő!

III. megoldás ötlete

Vizsgáljuk meg, hogy az egyik szakaszból a (rá következő, illetve a) második rá következő milyen transzformációval kapható. Mutassuk meg, hogy 5 ilyen transzformáció kompozíciója az identitás.

Lásd még Hraskó András doktorijának 1. fejezetét!

5. feladat

Határozzuk meg az összes olyan, nem azonosan nulla P(x) polinomot, amelyre

a) P(x²) º (P(x))²;

b) P(x²- 2x) º (P(x-2))²;

a) megoldása

Legyen P(x) = a_nxⁿ+..., ahol a_n a legmagasabb fokú tag együtthatója (tehát a_n ¹ 0).

P(x²) = a_nx²ⁿ+..., míg (P(x))² = a_n²x²ⁿ+..., így a_n = 1.

Látni fogjuk, hogy a megoldások a P(x) = xⁿ polinomok. Legyen ezzel ellentétben

P(x) = xⁿ+ a_kx^k + ..., ahol a_k a következő nemnulla együttható. Ekkor

P(x²) = x²ⁿ+ a_kx^2k + ..., míg (P(x))² = x²ⁿ+ 2a_kx^n+k + ..., így ilyenkor nincs azonosság.

Végül P(x) = xⁿ nyilván minden nemnegatív egész n-re megfelel.

b) megoldása

P(x) = 1 és P(x) = x+ 1 jó. Ötlet: próbáljuk visszavezetni az a) részre!

Legyen x – 1 = y és Q(y) = P(y– 1)! Ekkor a

(P(x-2))² º (P(y-1))² º (Q(y))², míg P(x²- 2x) º P((x-1)²- 1) º P(y²- 1) º Q(y²),

tehát az a) feladatrész megoldása alapján Q(y) º yⁿ, azaz P(y– 1) º yⁿ, tehát P(t) º (t+1)ⁿ.

6. feladat

Oldja meg az x⁶ + x³y = y³ + 2y² egyenletet az egész szám(pár)ok körében!

I. megoldás

Fejezzük ki x³-t y-nal!

A diszkriminánsra vezessünk be új ismeretlent: a² = 4y + 9, ahol a-ról feltehető, hogy nemnegatív egész. Fejezzük ki x³-t a-val! A gyök pozitív előjelénél:

amiből adódik, hogy a páratlan. Másrészt

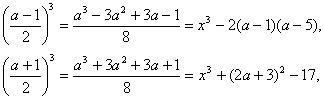
így

kivéve, ha a =1, 3 vagy 5. Ezeket az eseteket ellenőrizve és a negatív gyököt hasonlóan becsülve adódnak a megoldások:

x	0	0	2
y	0	-2	4

II. megoldás

Legyen x³ = z. Vegyük észre, hogy a p(z, y) = 0 harmadrendű görbének szinguláris pontja van az origóban. Magyarul: az y = mz egyeneseknek a 0 mindig kétszeres gyöke:

Fejezzük ki a harmadik metszéspontot m-mel!

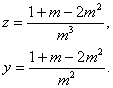
A p(z, y) görbe racionális pontjai egy-egyértelmű megfeleltetésben állnak m racionális értékeivel. Helyettesítsünk m helyére q/r-t és z-re írjuk fel, hogy z = x³!

(xp)³ = q³ + q²p – 2qp².

A p-vel való oszthatóság miatt (feltehető, hogy p és q relatív prímek és p>0) p = 1, tehát

x³ = q³ + q² – 2q.

|q| > 2 esetén

q³ < q³ + q² – 2q = x³ < (q+1)³,

ilyenkor tehát nincs megoldás. A többi esetet végignézve adódnak a megoldások:

x	0	0	2
y	0	-2	4

Gyakorolni valók:

6.2. Oldjuk meg az x⁶ + 3x³ + 1 = y⁴ egyenletet az egész szám(pár)ok körében!

6.3. Oldjuk meg az x² + xy + y² = x²y² egyenletet az egész szám(pár)ok körében!

2005. április 15.

A szakkörön ott voltak a Gillis-Turán verseny résztvevői, így a szakkör angol nyelven folyt. Az első részben Dobos Sándor extremális gráfokkal kapcsolatos feladatai szerepeltek, aztán Kós Géza tartott előadást. A feladatokat itt is angolul közöljük.

Az Ex(n, x-részgráf)=k jelölés azt jelenti, hogy egy n pontú egyszerű gráfnak legfeljebb k éle lehet, ha nincs benne x-részgráf.

1. Determine the following numbers:

(a) Ex(10, 3-star) (b) Ex(10, 3-path) (c) Ex(10, K₃)

2. Generalise the previous problem for n and k instead of 10 and 3.

3. G is a simple graph with 10 points. The degree of each point is greater than 3. Prove that there is an even circle in G.

4. G is a simple graph with 14 points. The points are distributed into three classes. Two points are connected iff they are in different classes. At most how many edges are there in G?

5. On the circumference of a circle are 21 points. Prove that among the arcs which join any two of these points, at least 100 of them must subtend an angle at the centre of the circle not exceeding 120°.

6. A pocket radio is operated by two AA batteries. In the drawer, we have 8 batteries, four of which are flat. Unfortunately, we do not know which four. The only way we can test the batteries is by inserting two of them in the radio set. If the radio is operating, both batteries are good, otherwise at least one of them is flat. What is the minimum number of trials needed in order to be certain that the radio will operate?

7. Suppose G is a simple graph, with 10 points. Among any 5 of the vertices there are at least 2 edges. At least how many edges are there in G?

8. Suppose G is a simple graph, with 10 points and some edges. We colour all of these edges with red or blue. How many edges may G have at most if there are no unicolour triangle in it?

9. Ten points are marked in the plane so that no three of them lie on a line. Each pair of points is connected with a segment. Each of these segments is painted with one of k colours, in such a way that for any k of the ten points, there are k segments each joining two of them and no two being painted with the same colour. Determine the smallest k for which this is possible.

2005. április. 29.

A szakkör a Gillis-Turán verseny feladatainak megbeszélésével kezdődött. Ezek a következők voltak:

1.) A derékszögű ABC háromszög AB átfogójára és BC befogójára “kívülről” megrajzoltuk a c, illetve az a négyzeteket. A C ponton és a c négyzet A-val összekötött csúcsán átmenő egyenes legyen e, az A ponton és az a négyzet B-vel összekötött csúcsán átmenő egyenes pedig legyen f.

Bizonyítsuk be, hogy az e és az f egyenesek egy olyan négyzet kerületén metszik egymást, amelynek csúcsai az ABC háromszög kerületén vannak.

2. Az f függvény egy adott H halmaz minden egyes részhalmazához a H egy-egy részhalmazát rendeli. A függvény monoton, tehát ha , akkor .

Bizonyítsuk be, hogy létezik a H halmaznak olyan részhalmaza, amelyre f.

3.) Keressünk olyan különböző pozitív egész számokat, amelyekre teljesül, hogy

.

4.) Meg lehet-e adni 2005 szomszédos pozitív egész számot úgy, hogy pontosan 25 prímszám forduljon elő közöttük?

5.) Legyen az kezdeti feltétellel megadott Fibonacci sorozat n-edik tagja. Tekintsük az és a függvényeket, ahol az utóbbi formulában darab 1-es szerepel.

Bizonyítsuk be, hogy minden valós x számra .

6.) Egy szabályos hétszög alapú terület csúcsaiban egy-egy oszlop áll. Minden egyes rúd tetejét egy egyenes huzal köti össze a két másodszomszédos rúd tetejével oly módon, hogy felülről nézve minden egyes huzal két másikat metsz.

Meg lehet-e választani az egyes oszlopok magasságát úgy, hogy semelyik négy oszlop teteje ne legyen egy síkban, továbbá valamennyi huzal egyszer felülről, egyszer pedig alulról haladjon át a megfelelő két kereszteződésen?

A szakkör hátralevő részében a 98-as olimpia első két feladatával foglalkoztunk:

7. Az ABCD konvex négyszög belső pontja P, AP=BP és CP=DP. Az AC és BD átlók merőlegesek. Igazoljuk, hogy az ABP és PCD háromszögek területe akkor és csak akkor egyenlő, ha ABCD húrnégyszög.

8. Egy versenyen a versenyző és b bíró volt, b>2 páratlan szám. A bírók minden versenyzőt megfelelt, vagy nem felelt meg minősítéssel értékeltek. Bármely két bíró legfeljebb k versenyzőt értékelt azonos módon. Igazoljuk, hogy .

2005. május 13.

Jankó Zsuzsi és Mészáros Gábor röviden beszámoltak a Balkán Olimpiáról ill. az olasz OKTV és csapatversenyről.

1. Az ABC háromszög beírt köre az AB és AC oldalakat D és E pontokban érinti. Igazoljuk, hogy az AB oldallal párhuzamos középvonal egyenese, a DE egyenese és a B-ből induló szögfelező egy ponton mennek át.

2. Határozzuk meg a pozitív valós számok halmazán értelmezett összes olyan pozitív értékű f függvényt, amely kielégíti a következő feltételeket: (1) f(xf(y))=yf(x) minden pozitív x, y számra; (2) f(x) 0-hoz tart, ha x tart a végtelenhez.

3. Az egy síkban fekvő O és K középpontú körök metszik egymást, egyik metszéspontjuk A. Közös érintőik az egyik kört P és Q, a másik kört R és S pontokban érintik. A PQ és RS szakaszok felezőpontjai M és N. Igazoljuk, hogy .

4. Kiválasztható-e a százezernél nem nagyobb pozitív egészek közül 2005 különböző szám úgy, hogy közülük semelyik három se alkosson számtani sorozatot?

5. Az ABC szabályos háromszög kerületének minden pontja piros vagy kék. Igazoljuk, hogy ekkor kiválasztható a kerületen három azonos színű pont, melyek derékszögű háromszöget alkotnak.

6. Jelölje a, b, c egy háromszög oldalainak hosszát. Igazoljuk, hogy

Házi feladatként kiosztottam a Balkán Olimpia feladatait, melyek a következők voltak:

7.

8. Határozzuk meg az összes olyan p prímszámot, amire p²–p+1 egy egész szám köbe.

9. Legyenek a, b, c pozitív valós számok. Bizonyítsuk be a következő egyenlőtlenséget:

.

Határozzuk meg, mikor áll fenn egyenlőség.

10.