Olimpiai szakkörök 2006 őszén:

szeptember 22, október 5, 20, november 10, 24, december 8.

2006. szeptember 22.

A szakkör elején felírtam a táblára a 7. és 8. feladatokat. Ezek közel olimpiai nehézségűek. Utána következtek az év eleji bemelegítő kisebb feladatok (1-6), ezeken dolgoztunk és megbeszéltük őket. A szakkör végén oldottuk meg az elején kitűzött két nehezebb példát (7-8).

1. Igazoljuk, hogy végtelen sok egész megoldása van a következő egyenletnek:

.

2. Az ABCD négyzet BC oldalának pontja K. A szögfelezője a CD oldalt M-ben metszi. Igazoljuk, hogy AK=DM+BK.

3. Örzse, Erzsi és Rezső szavakat írtak a füzetükbe, Örzse írta a legtöbbet, Erzsi a legkevesebbet. A szavakért pontokat kaptak. Ha egy szót csak egy valaki írt, azért két pontot kapott. Ha egy szót ketten is leírtak, azért mindketten egy-egy pontot kaptak. A mindhármuk által leírt szavakért nem járt pont. Lehetséges-e, hogy Erzsinek lett a legtöbb pontja és Örzsének a legkevesebb?

4. Két kör metszi egymást az A és B pontokban. Egy közös érintőjük az elsőt C-ben, a másodikat D-ben érinti, . A CB egyenes a második kört még E-ben is metszi. Igazoljuk, hogy szögfelezője AD.

5. Minden négyjegyű számnál tekintsük számjegyeinek szorzatát. Mennyi ezeknek a szorzatoknak az összege?

6. Egy O csúcsú szög egy-egy szárán találhatóak az AB és CD szakaszok, az A pont O és B között, a C pont O és D között van. Az AD és BC szakaszok felezőpontjain áthaladó egyenes AB-t M-ben, CD-t N-ben metszi. Bizonyítsuk be, hogy

.

7. Egy kocka lapjait fehérre és feketére festettük. Van egy sakktáblánk, amelynek mezői éppen akkorák, mint a kocka egy lapja. A kockát a sakktábla egy mezőjére helyezzük, majd végiggörgetjük a táblán úgy, hogy minden mezőre pontosan egyszer kerüljön. Lehetséges-e, hogy minden alkalommal a kockán levő alsó mező színe megegyezzen a sakktábla éppen alatta levő mezőjének színével?

8. Egy szög szárait érinti az O középpontú kör. Az egyik szögszárra tükrözzük O-t, így kapjuk az A pontot. A körhöz A-ból húzott érintők a szög másik szárát B és C pontokban metszik. Igazoljuk, hogy az ABC háromszög köréírt körének középpontja az eredetileg adott szög szögfelezőjén van.

Házi feladat:

9. Egy szabályos háromszögre oldalaival párhuzamos egyeneseket rajzolunk, amelyek az oldalakat 10 egyenlő részre, a háromszöget pedig 100 egybevágó kis háromszögre osztják. Megrajzoljuk még a háromszög oldalegyeneseit is. Két szomszédos párhuzamos közötti részt nevezzük sávnak. Legfeljebb hány kis háromszög jelölhető ki úgy, hogy semely két kiválasztott se essen egy sávba?

2006. október 5.

Ezt a szakkört Kós Géza tartotta.

1. Legyenek különböző valós számok.

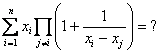
2. Mutassuk meg, hogy ha x,y>1, akkor

3. Bizonyítsuk be, hogy ha 0≤ x,y≤1, akkor

4. Igazoljuk, hogy ha a,b,c>0, akkor

5. Az pozitív számokra

.

Bizonyítsuk be, hogy

6. Bizonyítsuk be, hogy különböző pozitív egészek, akkor

7. Az a,b,c pozitív valós számok reciprokainak összege 1. Igazoljuk, hogy

8. Egy háromszög oldalai a,b,c. Mutassuk meg, hogy

9. Legyen k pozitív valós szám, n pozitív egész. Oldjuk meg az alábbi egyenletrendszert:

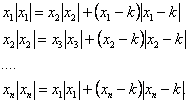
2006. október 20.

1. Igazoljuk, hogy végtelen sok egész megoldása van a következő egyenletnek:

.

2. Hat dobókockát kifúrtunk egy-egy szemköztes lapjuk középpontján át, majd egy rudat dugtunk a lyukakon át. Minden kocka szabadon forgatható a rúdon. Igazoljuk, hogy a kockákat beforgathatjuk úgy, hogy egy asztalra helyezve a legfelső lapok számai által alkotott hatjegyű szám osztható legyen héttel. (A kockák 1-től 6-ig számozottak, a szemköztes lapokon a számok összege 7.)

3. Összeszorozzuk az összes különböző olyan számot, melyet az alábbi kifejezésből kaphatunk, az előjelek lehetséges kiválasztásaival:

.

Bizonyítsuk be, hogy az eredmény négyzetszám.

4. Egy -as sakktábla minden mezőjét valamilyen színnel kifestettük úgy, hogy minden mezőnek legalább két oldalszomszédja vele azonos színű. Legfeljebb hány színt használhattunk fel?

5. Legyenek a, b, c valós számok. Bizonyítsuk be a következő egyenlőtlenséget:

.

6. Egy egységoldalú négyzetet téglalapokra vágtunk. Minden téglalapnak tekintjük a rövidebb oldalát, ha téglalapunk egy kis négyzet volt, annak az oldalát. Bizonyítsuk be, hogy ezek összege legalább 1.

Házi feladat:

7. Az ABCD konvex négyszög belső pontja M, AM=MB és CM=MD, továbbá . Bizonyítsuk be, hogy létezik olyan N pont, amelyre BNC és DNA szabályosak.

8. Egy énekversenyen 8 énekes vett részt. Összesen d dalt énekeltek, mindegyiket négyen adták elő és bármely két énekes ugyanannyi dalt adott elő közösen. Mi a legkisebb d, amire ez lehetséges?

2006. november 10.

1. Adott két pozitív egész m és n. Nevezzünk egy sakkfigurát

(n,m)-krokodilnak, ez n mezőt lép vízszintesen, vagy

függőlegesen, majd m mezőt erre merőleges irányban. Bizonyítsuk

be, hogy egy végtelen sakktábla kiszínezhető fehérre és feketére

úgy, hogy a figura minden lépése során az indulómezőtől különböző

színű mezőre lép.

2. Adott két ugyanakkora kör. Húzunk a középpontjaikat összekötő

egyenessel egy párhuzamos AB szakaszt úgy, hogy az A és B

között messe a köröket. A-ből érintőket húzunk a hozzá

közelebbi körhöz, ugyanígy B-ből érintőket húzunk a hozzá

közelebbi körhöz. Kiderült, hogy a négy érintő alkotta négyszög

tartalmazza mindkét kört. Igazoljuk, hogy az érintők alkotta

négyszögbe kör írható.

3. Van 20 gyöngyünk, 10 féle színben, minden színből éppen kettő

van. Beletettük a gyöngyöket 10 dobozba kettesével úgy, hogy

kiválasztható minden dobozból egy-egy gyöngy, hogy mind a tíz szín

előforduljon a kiválasztottak között. Igazoljuk, hogy az ilyen

kiválasztások száma 1-nél nagyobb kettőhatvány.

4. Az ABC háromszög beírt köre az AB és AC oldalakat rendre

a P, Q pontokban érinti. Az AC és BC oldalak

felezőpontjai rendre R és S. A PQ és RS egyenesek

metszéspontja T. Bizonyítsuk be, hogy BT felezi az ABCÐ

szöget.

5. Egy téglatest egy csúcsból induló éleinek hosszát összeadjuk

és ezt nevezzük a téglatest méretének. Lehetséges-e, hogy egy

téglatest tartalmaz egy önmagánál nagyobb méretű téglatestet?

6. Egy fekete egységoldalú szabályos háromszög van a síkon.

Hogyan helyezhető el 9 egységoldalú szabályos háromszög úgy, hogy

ezek ne fedjék egymást és mindegyik letakarja a fekete háromszög

valamely belső pontját?

2006. november 24.

A szakkörön a 93-94-es tanév OKTV feladatai közül oldottunk meg néhányat.

1. Egy egység oldalú négyzetben két kör helyezkedik el, amelyeknek nincs közös belső pontja (egymást kívülről, ill. a négyzet határát belülről érinthetik). Mennyi a kerületük összegének a lehető legnagyobb értéke?

2. Hány olyan legfeljebb 10-jegyü pozitív egész szám van, amely osztható négyzetgyökének (alsó) egészrészével? (Pl. a 12 ilyen, mert osztója a 12-nek, de a 22 nem ilyen, mert
nem osztója a 22-nek.)

3. Eszternek és Zsófinak 3−3 forintja van. Egy szabályos érmével dobálnak, fej esetén Eszter kap Zsófitól 1forintot, írás esetén pedig Zsófi kap Esztertől 1 forintot. Addig játszanak, amíg valamelyikük pénze elfogy. Mennyi a valószínűsége annak, hogy legalább 100 dobásra sor kerül?

4. Legyen f olyan nemkonstans valós együtthatós polinom, amellyel minden x, y valós számra

teljesül. Mutassuk meg, hogy f-nek pontosan egy valós gyöke van.

5. Egy 1993 szögpontú teljes gráf minden élét színezzük úgy, hogy semelyik csúcsba sem fut két azonos színű él. Bizonyítsuk be, hogy ekkor van 17 olyan pont, amelyek közül bármelyik kettőt különböző színű él köt össze.

6. Tekintsük az 1994 dimenziós vektorokat, azaz azokat az ( a₁ ,a₂ ,...,a₁₉₉₄ ) szám-1994-eseket, ahol az a_i ,,koordináták" tetszőleges valós számok. Nevezzünk egy ilyen vektort ,,bumfordi"-nak, ha a koordinátái között legfeljebb két különböző érték fordul elő (azaz például minden koordinátája −1 vagy √2 ). Legkevesebb hány bumfordi vektor összegeként állítható elő az (1, 2, ..., 1994) ?

(A vektorok összeadását koordinátánként értelmezzük, azaz két vektort úgy adunk össze, hogy a megfelelő koordinátákat összeadjuk.)

7. Egy tetszőleges m pozitív egészhez vegyünk minden lehetséges módon olyan a₁ < a₂ < ... < a_t egészeket, amelyekre a₁ = m és az a₁ a₂ ...a_t szorzat négyzetszám (t=1 is megengedett). Jelöljük S(m)-mel a_t lehető legkisebb értékét. Például S(1)=1, S(2)=6 mert m=2 esetén a 2×3×6 szorzat a legjobb választás, S(3)=8, S(4)=4 stb.

Bizonyítsuk be, hogy az S(2), S(3), S(4), … sorozatban éppen a pozitív összetett számok szerepelnek, éspedig mindegyik pontosan egyszer fordul elő.

2006. december 15.

1. 1. Bizonyítsuk be, hogy bármely a,b,c pozitív egészre (a;b)(a;c)[b;c] osztója abc-nek.

2. Legyenek x₁, x₂, x₃, x₄, x₅ pozitív valós számok. Bizonyítsuk be, hogy

3. Adott N és k pozitív egészekre megszámoltuk, hogy az N számot hányféleképpen lehet felírni a+b+c alakban, ahol 1a,b,ck, és az összeadandók sorrendje is számít. Kaphattunk-e eredményül 2006-ot?

4. Egy nem szabályos háromszög köréírt körének középpontja O, az oldalegyeneseket érintő körök középpontjai: A₁, A₂, A₃, A₄. Bizonyítsuk be, hogy az A_i, A_j, A_k pontok OA_n egyenestől mért előjeles távplságainak az összege nullával egyenlő; (i,j,k,n az 1,2,3,4 számok tetszőleges permutációját jelentik. Két pontnak egy egyenestől mért távolsága akkor azonos előjelű, ha az egyenesnek ugyanazon az oldalán vannak.)

5. Bálint 200 Ft-ot fizet Annának, ha a lottón a kihúzott számok szorzatának utolsó számjegye 0 lesz, különben Anna fizet Bálintnak 300 Ft-ot. Hosszabb távon kinek előnyös ez a megállapodás?

6. Jelölje k(n) az n pozitív egész legnagyobb páratlan osztóját és legyen A(n)=k(1)+k(2)+.....+k(n), B(n)=1+2+....+n. Mutassuk meg, hogy a 3A(n)=2B(n) egyenlőség végtelen sok n-re teljesül.