Olimpiai szakkörök 2008 januártól:

 Január 11.  25;  február 8. 22;  március 7. március 28. április 18.

 

2008. január 11.

 

1.         Tekintsük azokat a konvex négyszögeket, amelyek 100 darab egységnyi oldalú szabályos háromszögre darabolhatók.  Mekkorák lehetnek a megfelelő négyszögek oldalai?

2.         Adott egy egységnyi oldalú négyzet.  Határozzuk meg a négyzet síkjában levő azon körök középpontjainak a halmazát (mértani helyét), amelyeknek a négyzet mind a négy oldalával két közös pontja van.

3.         Az a, b, c, d pozitív egészekre ab=cd.  Lehet-e a+b+c+d prím?

4.         Van-e olyan gömb, amelynek egyetlen pontjára igaz, hogy mindhárom koordinátája racionális?

 

5.         Az 1, 2, …, N számok mindegyike piros, vagy zöld.  Egyszerre három szám színét megváltoztathatjuk, ha számtani sorozatot alkotnak.    Mely N-re érhető el bármilyen színezésről indulva, hogy minden szám piros legyen?

6.         Az ABCD konvex négyszög megfelelő csúcsainál meghúztuk a külső szögfelezőket, ezek a, b, c, d.  Metszéspontjaik    .  Tudjuk, hogy a K-ból AB-re, L-ből BC-re, M-ből CD-re bocsátott merőlegesek egy ponton mennek át.  Bizonyítsuk be, hogy ABCD húrnégyszög.

7.         Az a, b, c valós számokat úgy választottuk, hogy pontosan egy olyan négyzet van, melynek minden csúcsa rajta van az  függvény grafikonján.  Igazoljuk, hogy a négyzet oldala .

 

2008. január 25.

1.         Leírjuk egy sorba a következő számokat:      1,    1/2,    1/3,    1/4,    …..,    1/1993. 
A következő sorba  a szomszédosak különbségeit:     1/2,    1/6,    ……,     1/(1992·1993).  Így folytatva minden sorban egyel kevesebb szám lesz.  Mely szám áll az utolsó sorban egyedül?

2.         Az ABC háromszög AB oldalára kifele rajzolunk egy O középpontú négyzetet.  Legyenek M és N rendre a BC és AC oldalak felezőpontjai.  BC=a és AC=b rögzített,  a C-nél levő szög változhat.  Legfeljebb mekkora lehet OM+ON?

3.           Mutassuk meg, hogy létezik 100 különböző egész olyan sorozata,  hogy bármely kettő szomszédosnak négyzetösszege négyzetszám legyen.

4.           Egy egyenesen van balra egy piros, jobbra egy kék pont.  Bejelölhetünk két új, szomszédos pontot azonos színnel, vagy törölhetünk két meglévő szomszédos azonos színű pontot.  Mutassuk meg, hogy nem maradhat a végén csak két pont úgy, hogy balra egy kék, jobbra pedig egy piros.  (Szomszédos két pont, ha nincs köztük más jelölt pont.)

 

5.         Bergengóciában 2005 város van.  Fejletlen a csőpostahálózat;  semelyik két várost nem köti össze közvetlen cső.  Az új szabályok értelmében kiépíthetnek közvetlen csőkapcsolatot az A és B város között, ha létezik még két további város C és D úgy, hogy nincs közvetlen csőposta sem A és C, sem C és D, sem D és B között.  Legfeljebb hány csövet építhetnek ki?

6.         A hegyesszögű ABC háromszögben .  A köréírt kör középpontja O, az AO egyenes D-ben metszi BC-t.  Az ABD és ACD háromszögek köréírt köreinek középpontjai rendre E és F.  A B és C kezdőpontű BA és CA félegyeneseken van rendre G és H úgy, hogy AG=AC és AH=AB.  Igazoljuk, hogy EFGH akkor és csak akkor téglalap, ha .           

7.         Legyen p egy 2-nél nagyobb prím.  A  pozitív egészek a1, a2, …, ap-2   sorozatáról tudjuk, hogy p nem osztja sem ak-t, sem (akk–1)-et  (k=1,2, …, p–2).  Igazoljuk, hogy a sorozat néhány tagjának szorzata 2 maradékot ad p-vel osztva.

 

2008. február 8.

1.         Két parabola adott a síkon, tengelyeik merőlegesek és négy pontban metszik egymást.  Igazoljuk, hogy ez a négy pont húrnégyszöget alkot.

2.         16000-nek legfeljebb hány osztója adható meg úgy , hogy egyik sem osztja valamelyik másikat?  Gondoljuk meg ugyanezt 900-ra, 27 000-re.

3.         Az ABC háromszög AB oldalán adott a P pont, ezen keresztül párhuzamost húzunk a másik két oldallal.  Ezek AC-t és BC-t M és N pontokban metszik.  Szerkesztendő P, amelyre MN a legrövidebb.

4.         Adjunk meg olyan x-et, amelyre .  Igazoljuk, hogy x irracionális.

5.         Igazoljuk, hogy az  előáll két mon. növő polinomfüggvény különbségeként.  " polinom előáll?

6.         Igazoljuk, hogy tetszőleges pozitív a, b, c, d számokra .

7.         Az 1 sugarú körbe írt sokszög oldalainak négyzetösszege mely sokszög esetén lesz  legnagyobb?

8.         a, b, c, d olyan nemnegatív valós számok, melyekre .  Igazoljuk a következő egyenlőtlenséget:

9.         Egy 2005×2005-ös táblázat elemei az {1, 2, …, n} halmazból valók.  Az i-dik sor elemei alkotják az Xi halmazt, a j-dik oszlop elemei alkotják az Yj halmazt.  Melyik az a legkisebb n érték, melyre lehetséges, hogy az X1, X2, …, X2005, Y1, Y2, …, Y2005 halmazok páronként különbözők?

 

2008. február 22.

1.         Két önmagát nem metsző hétszög csúcsai azonosak, nincs közös élük.  Lehetnek-e egybevágóak?  Három hétszögre ugyanez.

2.         Adott 100 pont a síkon, nincs 3 egy egyenesen.  Igazoljuk hogy rajzolható 20 olyan diszjunkt konvex négyszög, amelynek csúcsai az adott pontok közül valók.  Rajzolható 22 is?

3.         Adjunk meg 8 pontot a síkban, amelyek közül nincs 3 egy egyenesen és semely 5 nem alkot konvex ötszöget.

4.         Egy gráf lerajzolását nevezzük kötésnek, ha bármely két élnek pont egy közös pontja van. (Az aB élen nem lehet a gráfnak további csúcsa.) Ez lehet végpont, vagy metszéspont, „érintési” pont nem.  Adjunk meg n pontú, n élű kötést.  Adjunk meg n pontú n élű kört.  (Tudomásom szerint megoldatlan, hogy lehet-e kötésnek n-nél több éle.)

5.         Egy geometriai gráfban minden él szakasz.  Ha n pontja van a síkban, hány éle lehet, ha bármely kettőnek pontosan egy közös pontja van?

 

6.         Az ABC szabályos háromszög belső P pontjának az oldalaktól vett távolságai .  Határozzuk meg azon P pontok mértani helyét, amelyre a p, q, r szakaszokból háromszög szerkeszthető.

7.         Legyen  kölcsönösen egyértelmű leképezés.  Igazoljuk, hogy van olyan , kölcsönösen egyértelmű leképezések, amelyekre f=u+v.

8.         Legyen a>1 pozitív egész.  Bizonyítsuk be, hogy bármely N egésznek van többese a következő sorozatban:  .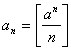

 

 

 2008. március 7.

1-2-3 és 4-5-6 az OKTV döntők feladatai II. és III. kategóriából

7.         Határozzuk meg   maximumát, ahol az xi –k nemnegatív számok és összegük 1-gyel egyenlő.

8.         Az R sugarú gömbbe írt ABCD tetraéderek közül melyikre a legkisebb az AB2+AC2+AD2-BC2-CD2-DB2  összeg és mekkora ez az érték?

9.         Egy vacsorára sütemény készül, a vacsorán várhatóan p vagy q személy fog résztvenni, (p,q)=1.  A süteményt szokás szerint egy téglalap alakú tepsiben sütik meg.  Legalább hány, nem feltétlenül egyforma részre kell vágnunk a süteményt, ha azt akarjuk, hogy a teljes sütemény szét legyen osztva és minden vendég egyenlő mennyiségű süteményt kapjon, bármelyik is következik be a két lehetőség közül?

 

2008. március 28.

 

2008. április 18.

1.         Egy egyirányú utcában n parkolóhely van egymás után.  Az utca n autós lakója este munkából jövet elhajt a kedvenc helyéig és ott parkol.  Ha foglalt, tovább megy és az első üres helyre beáll.  Amennyiben kedvenc helye foglalt és utána sincs üres hely, akkor vadul dudálni kezd.  Hányféle lehet a sofőrök kedvenc helyeinek listája, ha soha nem veri fel ádáz dudaszó a környéket?

2.         Biz. nincsenek olyan k, m nemnegatív egészek, melyekre .

3.         Szerkesszünk háromszöget, ha adott a BC oldal, a hozzá tartozó súlyvonal és a B és C csúcsnál levő szögek különbsége.