Olimpiai szakkörök 2009 januártól:
Január 9 és 23, február 6 és 20, március 6 és 20.
2009. január 9.
A szakkör feladatai: 2008/9-es OKTV II. kat 2. forduló és 2000/1-es OKTV III. kat döntő
1. Adjuk meg a valós számoknak azt a legbővebb részhalmazát,
melyen az f(x)
függvény értelmezhető és határozzuk meg a függvény értékkészletét ezen az értelmezési tartományon. ![]() .
.
2. Határozzuk meg a
következő egyenlet valós megoldásait: ![]() .
.
3. Egy 1 milliárd lakosú országban egy olcsó AIDS teszt bevezetését tervezik. Tudjuk, hogy kb. minden ezredik ember fertőzött. Kiderült, hogy a betegek 99,9\%-ánál pozitív, viszont sajnos az egészségesek 0,1\%-ánál is pozitív eredményt ad a teszt. Ilyen paraméterek mellett elvetették a használatát. Egy matematikus azt javasolta, hogy végezzék el kétszer egymás után a vizsgálatot és ha mindkettő pozitív, csak akkor küldjék orvoshoz a pácienst. Így már bevezethető lett a teszt. A következő két kérdéssel arra keressük a választ, mi ennek a magyarázata. (a) Számítsuk ki a valószínűségét, hogy beteg valaki, ha az első teszt pozitív. (b) Számítsuk ki a valószínűségét, hogy beteg valaki, ha mind a két teszt pozitív.
4. Az a, b, c
oldalú t területű hegyesszögű
háromszögre abc=a+b+c teljesül. Biz. be, hogy ![]() .
.
5. Legyen a c pozitív egész és jelölje c1, c3, c7 és c9 rendre a c azon pozitív osztóinak a számát, amelyek utolsó számjegye 1, 3, 7 ill.9. Bizonyítsuk be, hogy c1+c9³c3+c7.
6. Adottak a síkon a k1 és k2 körök, valamint a P
pont. Szerkesztendő olyan a P-n
átmenő e
egyenes, amely a köröket (i=1,2) Ai, Bi pontokban metszi úgy, hogy a ki körvonalak alkalmas Ci pontjaira ![]() teljesül. ( Nem szükséges annak diszkutálása, hány
ilyen e egyenes létezik, illetve létezik-e egyáltalán
ilyen e egyenes.)
teljesül. ( Nem szükséges annak diszkutálása, hány
ilyen e egyenes létezik, illetve létezik-e egyáltalán
ilyen e egyenes.)
7. Adott k+m darab különböző,
1-nél nagyobb egész szám, ![]() ahol mindegyik ai
páros sok, mindegyik bj
pedig páratlan sok (nem feltétlenül különböző) prím szorzata. Hányféleképpen lehet a k+m darab szám közül néhányat (akár egyet sem, akár az összeset)
kiválasztani úgy, hogy bármelyik bj-nek
(j=1, 2, …, m) a kiválasztott számok között páros
sok osztója legyen?
ahol mindegyik ai
páros sok, mindegyik bj
pedig páratlan sok (nem feltétlenül különböző) prím szorzata. Hányféleképpen lehet a k+m darab szám közül néhányat (akár egyet sem, akár az összeset)
kiválasztani úgy, hogy bármelyik bj-nek
(j=1, 2, …, m) a kiválasztott számok között páros
sok osztója legyen?
2009. január 23.
1. Biz. ![]() pozitív számokra
pozitív számokra ![]() .
.
2. Mely (x,y,z) pozitív
egészekre teljesül: ![]() ?
?
3. Határozzuk meg a legkisebb valós c számot, amelyre bármely háromszög kerületén van két pont, melyek a kerületet felezik és távolságuk nem nagyobb a kerület c-szeresénél.
4. Mely poz. prím valamely poz. eg. kitevős hatványa írható fel két pozitív egész köbének összegeként.
5. Van-e olyan f(x) egész együtthatós, 2009-edfokú polinom, amelyre bármely n egészre az f(n), f(f(n)), f(f(f(n))),… számok páronként relatív prímek?
6. Legyen n>2, az ![]() számok összege
pozitív. Ezen
számok egy
számok összege
pozitív. Ezen
számok egy ![]() permutációját jónak
hívjuk, ha
permutációját jónak
hívjuk, ha ![]() , k=1,2,…,n esetén. Legalább hány jó permutáció van?
, k=1,2,…,n esetén. Legalább hány jó permutáció van?
7. Az ABC háromszög
A, B, C
csúcsainak merőleges vetülete rendre a C,
A, B- ből induló külső szögfelezőre A’, B’, és C’.
Az A’B’C’ köréírt kör sugara d.
ABC háromszögbe írt kör sugara
r, félkerülete s. Biz. ![]() .
.
8. Adott egy ![]() pontú egyszerű gráf. (n=3k+1, k. poz.eg.).
Legalább hány éle van, ha bármely n
pont közt lesz négy, amely teljes négyes?
pontú egyszerű gráf. (n=3k+1, k. poz.eg.).
Legalább hány éle van, ha bármely n
pont közt lesz négy, amely teljes négyes?
2009. február 6.
A 2002-es IMO feladatai
2009. február 20
A 2003-as IMO feladatai
2009. március 6.
Az OKTV II és III kategória döntős feladatai
2009. március 20.
A Surányi János emlékverseny (első olimpiai válogató) feladatai:
1. A derékszögű koordinátarendszerben nevezzük doboznak az olyan téglalapokat, amelyeknek oldalai a tengelyekkel párhuzamosak. Ha két doboznak van közös belső, vagy határpontja, akkor őket metszőknek nevezzük.
Legfeljebb mekkora lehet n, ha megadható n doboz B1,B2,…,Bn úgy hogy Bi és Bj akkor és csak akkor metszők, ha n nem osztja sem i–(j+1)-et, sem i–(j-1)-et.
2. Az ABC háromszög beírt köre az AB és AC oldalakat rendre a D és E pontokban érinti. A beírt körnek és az AEB háromszög köré írt körnek E-től különböző közös pontja legyen F, a D pont merőleges vetülete az EB egyenesen G. Igazoljuk, hogy 2ABEÐ=BFGÐ.
3. Igazoljuk, hogy a 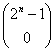 ,
,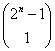 ,
,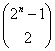 ,…,
,…,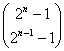 számok csupa
különböző, páratlan maradékot adnak
számok csupa
különböző, páratlan maradékot adnak ![]() -nel osztva.
-nel osztva.
Továbbá a Romániai Matematikai Mesterek verseny 2009 feladatai: