Olimpiai szakkörök 2011 januártól:
január 7 és 21, február 4 és 18, március 4 és 18, április 1 és 15. május 6.
2011. Január 7.
1. Egy tetraéder éleire valós számokat írtunk, a kitérő élekre írt számok összege ugyanannyi. Ezután minden csúcshoz hozzárendeltük az oda befutó élekre írt számok összegét. Ezek az összegek valamilyen sorrendben az a, b, c, és d számok, amelyekre a=b=2c=2d teljesül. Biz. az élekre írt számok között a 0 is előfordul.
2. Tekintsük az y=x2 parabolát. Keressük meg az összes olyan egész meredekségű egyenest, ami áthalad a P(0;4) ponton és a parabola belsejébe eső szakasza is egész hosszúságú.
3. Keressük meg a 2010-nél nagyobb egészek közt a legkisebb olyan S számot, amelyet elosztva a 3, 4, 5, 6, 7 és 8 számokkal, maradékul kétszer kapjuk az 1, 2, 3 számok mindegyikét.
4. Biz. a t területű ABCD konvex négyszög akkor és csak akkor téglalap, ha (AB+CD)(AD+BC)=4t.
5. Az ABC háromszögben AD és BE szögfelezők, D és E a kerületen van. Mekkora az A-nál levő szög, ha DE felezi az ADC szöget?
6. Tudjuk, hogy a, b, c pozitív számok, abc=1. Igazoljuk :
![]()
7. A síkon van véges sok, párhuzamos szélű sáv, összes szélességük 100. Mutassuk meg, hogy a sávok eltolhatók önmagukkal párhuzamosan úgy, hogy együtt letakarjanak egy adott, 1 sugarú kört.
8. Bergengóciában a lottón 6 számot húznak 36-ból. Hány szelvényt kell kitölteni a biztos betli szelvényhez?
2011. január 21.
1. Biz. ![]() . 6-os
példához:
. 6-os
példához: 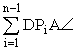
2. Elhelyezhető-e egy kocka úgy, hogy csúcsainak egy síktól való távolságai 0, 1, 2, 3, 4, 5, 6 és 7 legyen?
3. Bizonyítsuk, hogy a) 9797; b) 199717 nem lehet szomszédos természetes számok köbeinek összege.
4. Az ABC háromszög belső pontja P, AB=BC.
![]()
![]() ,
,![]() .
BPC Ð=?
.
BPC Ð=?
5. Egy súlykészletben a következő grammos súlyok vannak: 1, 2, 4, 8, 16, 32, 64, 128, mindből egy darab. A kétkarú mérlegünk mindkét serpenyőjébe tehetünk súlyokat. a) Biz. semelyik súlyt sem mérhetjük le több, mint 34 módon. b) Adjunk példát olyan súlyra, melyet 34 módon mérhetünk le.
6. Az ABC háromszögben AB=AC és a BAC szög α. Legyen D az AB szakaszon, AD=AB/n. Legyenek P1, P2. … , Pn-1 a BC oldal n-edelő pontjai. Mekkora lesz α függvényében a fenti szögösszeg, ha n=2011?
7. Van-e olyan hatjegyű pozitív egész, jelölje A, melyre az A, 2A, 3A,.....,500000A közt nincs olyan, mely hat azonos jegyre végződne?
8. Megadható-e egy poz. egészekből álló növő számtani sorozat a) 11; b) 10 000; c) végtelen sok egymást követő eleme úgy, hogy a számok jegyeinek összege is növő számtani sorozat szomszédos elemei legyenek?
9. Mutassuk meg, hogy nem létezik olyan függvény, melyre f(f(x))=x2-1996 minden valós x-re.
2011. február 4.
Ezt a szakkört Gyenes Zoltán tanár úr tartotta.
2011. február 18.
1. Az ABC háromszög AB oldalát kívülről érintő hozzáírt kör AB-t a P pontban, AC meghosszabbítását a Q pontban érinti; a BC oldalt kívülről érintő kör pedig AC meghosszabbítását az U pontban, AB meghosszabbítását az X pontban érinti.
Bizonyítsuk be, hogy a PQ és az UX egyenesek metszéspontja egyenlő távol van az AB és a BC egyenesektől.
2. Az a1, a2, ..., an és b1, b2, ..., bk pozitív egészek; az a1+a2+...+an és a b1+b2+...+bk összegek egyenlők, és kisebbek nk-nál (n>1, k>1). Bizonyítsuk be, hogy az a1+a2+...+an=b1+b2+...+bk egyenlőségben szereplő mindkét összegből elhagyható néhány (de nem az összes) tag úgy, hogy az egyenlőség továbbra is fennálljon.
3. Mutassuk meg, hogy egy páratlan fokú, egész együtthatós polinomfüggvény grafikonjában csak véges sokszor fordulhat elõ, hogy két (különbözõ) egész abszcisszájú pont távolsága egész szám.
4. Az ABC háromszög nem egyenlő szárú; a BC, CA, AB oldal felezőpontját jelölje rendre A1, B1, C1. A háromszög oldalain a C-ből az A-ba és onnan a B-be vezető út felezőpontja legyen A2, az A-ból a B-be és onnan a C-be vezető út felezőpontját jelölje B2, végül a B-ből a C-be és onnan az A-ba vezető út felezőpontja legyen C2. Bizonyítsuk be, hogy az A1A2, B1B2, C1C2 egyenesek egy ponton mennek át.
5. Legyen n rögzített, 1-nél nagyobb egész szám. Adjunk meg olyan x1, x2, ..., xn valós számokat, amelyekre teljesülnek az x1+x2+...+xn=2(n-1) és az (x1-1)2+ (x2-1)2+...+ (xn-1)2=n egyenlőségek, és xn értéke a lehető legnagyobb.
6. Tekintsük azt a kört, amely áthalad azon a három ponton, ahol egy adott háromszög szögfelezõi metszik a szemközti oldalakat. Bizonyítsuk be, hogy a háromszög oldalegyenesei ebbõl a körbõl három olyan húrt metszenek ki, amelyek közül valamelyiknek a hossza egyenlõ a másik kettõ hosszának az összegével. (Ha a kör a háromszög oldalegyenesét nem metszi, hanem érinti, akkor a megfelelõ húrt 0 hosszúságúnak vesszük.)
7. Van-e olyan n-oldalú sokszög, amelyben a hegyesszögek száma n2-30n+ 236?
2011. március 4.
Az OKTV II és III kategória döntőinek feladatait beszéltük meg
2011. március 18.
2011. április 1.
2011.május 6.
1. Egy nem szabályos háromszög köréírt körének középpontja O, az oldalegyeneseket érintő körök középpontjai: A1, A2, A3, A4. Bizonyítsuk be, hogy az Ai, Aj, Ak pontok OAn egyenestől mért előjeles távplságainak az összege nullával egyenlő; (i,j,k,n az 1,2,3,4 számok tetszőleges permutációját jelentik. Két pontnak egy egyenestől mért távolsága akkor azonos előjelű, ha az egyenesnek ugyanazon az oldalán vannak.)
2. Jelölje k(n) az n pozitív egész legnagyobb páratlan osztóját és legyen A(n)=k(1)+k(2)+.....+k(n), B(n)=1+2+....+n. Mutassuk meg, hogy a 3A(n)=2B(n) egyenlőség végtelen sok n-re teljesül.
3. Az ABC hegyesszögű
háromszög köréírt körének középpontja O, sugara R. Az AO egyenes a BOC kört A1-ben,
a BO egyenes a COA kört B1-ben, a CO egyenes az AOB kört C1-ben
metszi. Bizonyítsuk be, hogy ![]() .
.
4. Az a1, a2, ...., an
valós számokra ![]() , n ³3 teljesül.
Bizonyítsuk be, hogy ha a1+a2+....+an=s,
akkor
, n ³3 teljesül.
Bizonyítsuk be, hogy ha a1+a2+....+an=s,
akkor ![]() .
.
5. Jelölje A(n) az első n darab prímszám összegét. Bizonyítsuk be, hogy A(n) és A(n+1) között mindig van négyzetszám.
6. Egy sakk körmérkőzésnek k résztvevője volt (k páratlan); mindenki mindenkivel pontosan egyszer játszott; győzelemért 2, döntetlenért 1, vereségért 0 pontot kaptak. A verseny végén mindenkinek más volt az elért pontszáma. Legfeljebb mennyi lehetett a döntetlen játékok száma?
7. Az ABC háromszög beírt körének sugara legyen egységnyi. Jelölje ra az AB és AC oldalakat, valamint a háromszög köréírt körét belülről érintő kör sugarát; hasonlóan értelmezzük az rb és rc sugarakat is. Határozzuk meg ra+rb+rc minimumát.