Olimpiai szakkörök 2013-2014-as tanévben:

Szeptember 20; október 4 és 18;

2013. szeptember 20.

A szakkörön az olimpia első öt feladatát néztük át. A további feladatok maradtak házinak, ezek közül a 9. nehezebb, ez beadható papíron névvel a következő szakkörön.

1. Bizonyítsuk be, hogy bármilyen pozitív egész k és n számok esetén található k (nem feltétlenül különböző) pozitív egész: , amikre .

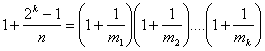2. A sík 4027 pontjából álló alakzatot nevezzük kolumbiainak, ha 2013 piros, a többi kék és az alakzat semely három pontja sincs egy egyenesen. Néhány egyenes meghúzásával a síkot tartományokra bontjuk. Az egyenesenek ezt az elrendezését a kolumbiai alakzatra nézve jónak nevezzük, ha semely egyenes sem megy át az alakzat egyetlen pontján sem és nincs olyan tartomány, amelyik mindkét színű pontot tartalmaz. Határozzuk meg a legkisebb olyan k értéket, amire igaz, hogy a 4027 pontból álló bármely kolumbiai alakzatra van k egyenesből álló jó elrendezés.

3. Az ABC háromszög A csúcsával szemközti hozzáírt köre érintse a BC oldalt az pontban. Hasonlóan definiáljuk a CA oldal és az AB oldal pontját. Tegyük fel, hogy az háromszög körülírt körének középpontja az ABC háromszög köré írt körön van. Bizonyítsuk be, hogy az ABC háromszög derékszögű.

4. Legyen az ABC hegyesszögű háromszög magasságpontja H és legyen W a BC oldal egy belső pontja. A B-ből ill. C-ből induló magasságok talppontjai legyenek M ill. N. Jelölje a BWN háromszög körülírt körét és legyen X az kör azon pontja, amire WX -nek átmérője. Hasonlóan, jelölje a CWM háromszög körülírt körét és legyen Y az kör azon pontja, amire a WY -nek átmérője. Bizonyítsuk be, hogy az X, Y, és H pontok egy egyenesen fekszenek.

5. Jelölje Q⁺ a pozitív racionális számok halmazát. Legyen f:Q⁺→R olyan függvény, ami kielégíti a következő három feltételt: (i) Minden x,y poz. rac esetén f(x)f(y)≥f(xy);(ii) Minden x,y poz. rac esetén f(x+y)≥f(x)+f(y); (iii)Létezik olyan a>1 racionális szám, amire f(a)=a. Bizonyítsuk be, hogy f(x)=x minden poz. rac. x esetén.

6. A síkon van 2n pont, nincs három egy egyenesen. Min hány egyenessel vágható fel a sík tartományokra úgy, hogy minden tartományban legfeljebb egy pont legyen?

7. Az ABC háromszög minden oldalát a k kör két pontban metszi. A’ és A” stb. Biz ha AA’, BB’ és CC’ egy ponton megy át, akkor AA”, BB” és CC” is.

8. Van-e olyan f: R→R függvény, amely bármely valós x-re kielégítik az (f(x²))² + f(2^x) + 1 = 0 összefüggést.

9. n×n-es táblába beírjuk 1től n²-ig a poz. egészeket. A szomszédos mezőkön levő számok eltérésének vesszük a legnagyobb értékét, legyen ez M. Mi M lehető legkisebb értéke? (A szomszédos csak oldalszomszédost jelent.)

2013. október 4.

A szakkör elején a legutóbbi feladatsor első 4 feladatát beszéltük meg, majd az alábbi példák közül az első négyet.

1. Adott a hegyesszögű ABC háromszög. Határozzuk meg a belsejében azon P pontok mértani helyét, amelyekre ABPÐ=ACPÐ és CBPÐ=CAPÐ.

2. Mely poz. egészeknek van olyan többese, amelyben csak a 3-as vagy 4-es számjegy fordul elő?

3. a,b,c nem neg. valósak, a+b+c=1. Biz. 7(ab+bc+ca)≤2+9abc.

4. Egy körvonal hat különböző pontja között 15 húr húzható. Igazoljuk, hogy a kör középpontját ezen húrokra tükrözve a tükörképek közül legalább Þ a körvonalon kívül esik.

5. Adott a síkon 10 pont, közöttük nincs három egy egyenesen. Minden pontpárt összeköt egy szakasz, amelyeket kiszínezünk k színnel úgy, hogy bármely k pontot választva, a köztük futó szakaszok között mind a k szín előfordul. Határozzuk meg azt a legkisebb k-t amelyre létezik ilyen színezés.

6. Biz. egy n pontú és m élű egyszerű gráf háromszögeinek száma legalább .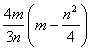

7. A térben felvettünk 2n pontot (n>1) úgy, hogy semely négy nem fekszik egy síkban, és megrajzoltunk a pontok között n²+1 összekötő szakaszt. Bizonyítsuk be, hogy a berajzolt szakaszok meghatároznak legalább n háromszöget.

A szakkör elején korábbi feladatok megbeszélése volt, ezért ezen feladatok nagy része későbbre maradt. (lásd november 29.)

2013. október 18.

Ezt a szakkört Hraskó András tanár úr tartotta.

A szakkör anyaga elérhető itt.

2013. november 15.

Ezt a szakkört Pelikán József tanár úr tartotta. A szakkörről felvétel készült ennek feldolgozása folyamatban van. Amint elkészül, elérhető lesz itt.

2013. november 29.

1. Egy körvonal hat különböző pontja között 15 húr húzható. Igazoljuk, hogy a kör középpontját ezen húrokra tükrözve a tükörképek közül legalább Þ a körvonalon kívül esik.

2. Legyen a G összefüggő gráf éleinek száma k. Bizonyítsuk be, hogy meg lehet az éleket számozni az 1, 2, …, k számokkal úgy, hogy minden olyan csúcs esetén, amelyből legalább két él indul ki, az illető csúcsokból kiinduló összes élhez rendelt számok legnagyobb közös osztója 1.

3. Egy 9 pontú gráf minden élét pirosra, kékre festjük, vagy színezetlenül hagyjuk. Melyik a legkisebb n, amelyre n színezett él esetén már biztosan lesz olyan háromszög, melynek minden éle ugyanolyan színű.

4. Egy nemzetközi társaságnak 1978 tagja van 6 különböző országból, a tagokat 1-től 1978-ig számozták meg. Mutassuk meg, hogy van legalább egy olyan tag, akinek a sorszáma megegyezik két honfitársa sorszámának az összegével, vagy kétszer akkora, mint egy honfitársa sorszáma.

5. Adott a síkon 10 pont, közöttük nincs három egy egyenesen. Minden pontpárt összeköt egy szakasz, amelyeket kiszínezünk k színnel úgy, hogy bármely k pontot választva, a köztük futó szakaszok között mind a k szín előfordul. Határozzuk meg azt a legkisebb k-t amelyre létezik ilyen színezés.

6. Biz. egy n pontú és m élű egyszerű gráf háromszögeinek száma legalább .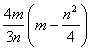

7. A térben felvettünk 2n pontot (n>1) úgy, hogy semely négy nem fekszik egy síkban, és megrajzoltunk a pontok között n²+1 összekötő szakaszt. Bizonyítsuk be, hogy a berajzolt szakaszok meghatároznak legalább n háromszöget.

2013. december 13.

A szakkört Pelikán József tanár úr tartotta.

2014. január 17.

A szakkört Kós Géza tanár úr tartotta.