Olimpiai szakkörök feladatanyaga a 2016-2017-os tanévben:
Olimpiai szakkör 2016. szeptember 16.
1. n ☺ a síkot tartományokra osztja. Színezhetők-e a tartományok két színnel úgy, hogy a szomszédosak különböző színűek? a) ☺=egyenes; b) ☺=kör; c) ☺= téglalap.
2. Biz: egy konvex sokszög akkor és csak akkor vágható szét egymást nem metsző átlókkal 3 szögekre úgy, hogy minden csúcsból páros számú átló induljon ki, ha a sokszög oldalszáma osztható 3-mal.
3. n egyenes út fut a síkon. A kereszteződésekben építhetők-e alul ill. felüljárók úgy, hogy minden egyenes mentén éppen felváltva következzenek?
4. Konvex 7-szög oldalai kül. hosszúak. Hányféleképpen vágható fel nem metsző átlókkal háromszögekre?
5. Legyen n legalább kettő. A sík n szakasza közül bármely kettő belső pontban metszi egymást, minden metszéspontban kettő találkozik. Jeromos minden szakasz egyik végére tesz egy békát, majd (n–1)-szer tapsol. Minden tapsolásra a békák a szakaszukon a következő metszéspontra ugranak. (a) Igazoljuk, hogy ha n páratlan, akkor Jeromos el tudja helyezni a békákat úgy, hogy ne találkozzanak. (b) Igazoljuk, hogy ha n páros, akkor bárhova is helyezte Jeromos a békákat, valamely taps után kettő találkozni fog.
6. Legyenek p és q rögzített relatív prím pozitív egészek. A nemnegatív egészek egy S részhalmazát ideális részhalmaznak nevezzük, ha a következő két feltétel egyszerre teljesül: (i) S tartalmazza a nullát; (ii) ha n eleme S-nek, akkor n+p és n+q is eleme S-nek. Határozzuk meg az S ideális részhalmazok számát. (p=5, q=7 esetén az első helyes válasz jutalmat kap!)
Olimpiai szakkör 2016. szeptember 30.
1. Egy sakktáblának melyik mezőjét elhagyva lesz a többi 63 mező lefedhető 1x3-as elemekkel?
2. Igazoljuk, hogy ha egy alakzat lefedhető csak S-tetrominókkal, akkor bárhogyan is fedjük le S- és Z-tetrominókkal, összesen páros sok Z-tetrominót fogunk felhasználni. (Az elemeket szabad elforgatni.)
3. Egy társaságban mindenki legfeljebb 3 másik emberrel van rosszban. Igazoljuk, hogy a társaság leültethető két asztalhoz úgy, hogy mindenki legfeljebb egy olyannal kerüljön egy asztalhoz, akivel rosszban van. (b) Mi a helyzet, ha a "rosszban levés" nem kölcsönös?
4. A táblára fel van írva egy nemnegatív egész számokból álló számnégyes. Egy lépésben az (a,b,c,d) számnégyest lecserélhetjük az (|a-b|,|b-c|,|c-d|,|d-a|)-re. Igaz-e, hogy tetszőleges kiindulásból véges sok ilyen lépés után eljutunk a (0,0,0,0)-ba? (b) És ha tetszőleges nemnegatív valósakból indulunk?
5. A rácssík (+,+) negyedének rácsnégyzeteiben játsszuk a következő játékot: Kezdetben 6 korong van elhelyezve, az (1,1), (1,2), (1,3), (2,1), (2,2) és (3,1) rácsnégyzetekben. (Mindig a jobb felső csúcs koordinátája van megadva.) Egy lépésben levehetünk egy korongot egy olyan négyzetből, aminek a jobb oldali és felső szomszédja is üres, viszont a jobb oldali és felső szomszéd négyzetekbe egy-egy új korongot kell tenni. Elérhető-e ilyen lépésekkel, hogy a kezdetben foglalt hat négyzet mindegyike üressé váljon? (b) Üressé tehető-e ez a hat mező, ha kezdetben csak az (1,1) rácsnégyzetben van korong?
6. A rácssík y≤0 félsíkjának tetszőleges rácspontjaira korongokat helyezhetünk. Ezután ha A, B, C olyan egy rácsegyenesre eső szomszédos rácspontok, hogy A-n és B-n van korong, C viszont üres, akkor megtehetjük, hogy az A-n lévő koronggal átugorjuk B pontot, B-ről pedig levesszük a korongot (így végül csak C-n lesz korong). Elérhető-e ilyen lépésekkel, hogy a (0,5) rácspontra kerüljön egy korong?
Olimpiai szakkör 2016. október 14.
1. Hány 9 betűs szó
van, amely
2. p(x) egészegyüthatós polinom, p(3)=p(7)=2. Van-e olyan egész k, amelyre p(k)=9?
3. (x–1)(x–2)…(x–2016)= (x–1)(x–2)…(x–2016) Szeretnénk minél kevesebb tényezőt letörölni úgy, hogy mindkét oldalon maradjon legalább egy, és az egyenletnek ne legyen valós gyöke.
4. Keressük p(x) polinomokat, ha minden valós x-re x×p(x–1)=(x–12)p(x) és p(12)=12!.
5. Határozzuk meg mindazon ![]() , a0≠0
egészegyütthatós polinomokat, amelyeknek gyökei éppen az ai számok (0£i£n–1).
, a0≠0
egészegyütthatós polinomokat, amelyeknek gyökei éppen az ai számok (0£i£n–1).
6. Lehet-e racionális az ![]() polinom mindhárom
gyöke?
polinom mindhárom
gyöke?
7. Oldjuk meg az egyenletrendszereket (a) x+y+z=–1; xy+yz+zx=–2; xyz=2. (b) x+y+z=2; x2+y2+z2=14 és x3+y3+z3=20.
8. Legyen n olyan
pozitív egész, amelynek köbgyöke nem egész. Igazoljuk, hogy egyetlen olyan 1
főegyütthatójú harmadfokú racionális együtthatós polinom van, amelynek gyöke a ![]() és ennek nincs több valós gyöke.
és ennek nincs több valós gyöke.
9. p(x) legalább másodfokú polinom. Készítsük el a qi(x) polinomsorozatot a következőképpen: q1(x)=p(x), qn+1(x)=p(qn(x)). Jelölje rn a qn gyökeinek az átlagát. Mekkora r99, ha tudjuk, hogy r19=99?
Olimpiai szakkör 2016. október 28.
1. Egy 10 elemű halmaznak legfeljebb hány részhalmazát (továbbiakban rh) választhatjuk ki, ha bármely két kiválasztottnak van közös eleme?
2. Egy külkereskedelmi vállalatnak 70 dolgozója van. Bármely két A és B dolgozóhoz van olyan nyelv, amelyen A beszél, de B nem és olyan is amelyen B beszél de A nem. Legalább hány különböző nyelvet beszélnek a vállalat dolgozói?
3. Az {1,2,3,…,10} minden rh-át leírjuk egy-egy piros cédulára. Vesszük sorra a piros cédulákat és mindegyiknek minden rh-át leírjük külön- külön egy fehér cédulára. Most vesszük sorra a fehér cédulákat és mindegyiknek minden rh-át leírjük külön- külön egy zöld cédulára. Hány zöld cédulánk lesz?
4. Az 1.-es feladat azzal a további feltétellel, hogy minden kiválasztott részhalmaz 4 elemű.
5. Egy 100 elemű halmaznak legfeljebb hány rh-át választhatjuk ki, ha bármely két kiválasztott vagy diszjunkt, vagy egyik tartalmazza a másikat?
6. Az {1,2,3,…,20017} halmaznak tekintjük a 77 elemű részhalmazait. Azok száma, amelyekben az elemek összege páros legyen p, amelyekben páratlan q. Melyik nagyobb? És mennyivel?
7. Egy feleletválasztós tesztvizsga 4 kérdésből állt. Minden kérdésre háromféle válasz volt adható. A vizsgán résztvevő diákokról kiderült, hogy bármely hármójukhoz volt olyan kérdés, amelyre mindhárman másképpen válaszoltak. Legfeljebb hány diák vehetett részt a vizsgán?
Olimpiai szakkör 2016. november 11.
1. Legyenek x, y és z
pozitív, 4-nél kisebb valós számok. Bizonyítsuk be, hogy az alábbi számok
között van olyan, amely nagyobb vagy egyenlő 1-nél. ![]()
2. Oldjuk meg az egész számok körében az ![]() egyenletet.
egyenletet.
3. Melyek azok a háromszögek, amelyekben az egyik csúcsból induló szögfelező egyenesére szimmetrikusan helyezkedik el az ugyanonnan induló súlyvonal és magasságvonal?
4. Igazoljuk, hogy " ![]() esetén S osztható m-mel.
esetén S osztható m-mel. 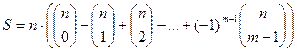
5.Határozzuk meg a legkisebb olyan c valós számot, amely rendelkezik az alábbi tulajdonsággal: Bármely háromszög kerületén található két pont, amelyek a háromszög kerületét felezik és a távolságuk nem nagyobb a kerület c-szeresénél
6. Bizonyítsuk be, hogy az ![]() pozitív számokra teljesül a következő egyenlőtlenség:
pozitív számokra teljesül a következő egyenlőtlenség: ![]()
7. Legyen c pozitív egész és jelölje c1, c3, c7, c9 rendre a c azon pozitív osztóinak a számát, amelyek utolsó jegye 1, 3, 7, 9. Bizonyítsuk be, hogy c1+c9³c3+c7.
Olimpiai szakkör 2016. december 9.
1. Igazoljuk, hogy végtelen sok olyan derékszögű háromszög van, amelyben az oldalhosszak relatív prím egész számok és az átfogó hosszából bármelyik befogó hosszát levonva egy-egy köbszámot kapunk.
2. Az ABC háromszög szögei Pi/7, 2Pi/7, 4Pi/7. A háromszög szögfelezői a szemközti oldalakat az A’, B’, C’ pontokban metszik. Mutassuk meg, hogy az A’B’C’ háromszög egyenlőszárú.
3. Egy k élhoszúságú kocka három egy csúcsba futó lapját teljesen le akarjuk ragasztani k2 darab 3×1 méretű címkével. Milyen k-ra lehet ezt megtenni?
4. Az ABC háromszögben AC≠3AB. A BC oldal felezőpontján át párhuzamost húztunk a BAC szög felezőjével, ez az AB és AC egyeneseket X és Y pontokban metszi. X tükörképe Y-ra legyen Z. BY és CZ eyenesek metszéspontja D. Igazoljuk, hogy BDC szög szögfelezője párhuzamos XY-nal.
5. Legyen p≡2 (mod3) páratlan prím. Legyen ak=k2+k+1. Bizonyítsuk be, hogy a1a2…..ap-1≡3 (mod p).
Olimpiai szakkör 2017. január 13..
1. Szerkesztendő háromszög, ha adott MA, MC és BC, ahol M a magasságpont.
2. Egy körvonal P pontjából indul két egyenlő hosszú húr, melyek 30°-os szöget zárnak be. Szerkesztendő a körnek olyan húrja, melyet az adott húrok három egyenlő részre osztanak.
3. Egy hegyesszögben adott a P pont. Csak vonalzóval szeretnénk meghúzni a P-n és a szög csúcsán áthaladó egyenes egy darabját, ha a szög csúcsát beragasztózták és nem férünk hozzá.
4. Szerkesztendő az ABC háromszög, ha adott BC, α és az A-ból induló belső szögfelező.
5. Legyenek AB és CD egy kör húrjai, amelyeknek nincs közös pontjuk, továbbá K a CD húr egy belsõ pontja. Szerkesszük meg a kör kerületén a P pontot úgy, hogy a CD húrnak az ABP háromszögbe esõ szakaszát a K pont felezze.
6. Adottak a k1 és k2 körök, továbbá a P pont. Szerkesztendő P-n át egy olyan szelő, amelyből a két kör ugyanolyan hosszú húrokat metsz ki.
7. Szerkesztendő a hegyesszögű ABC háromszög, ha adott a BC oldal F felezőpontja, a BB’ és CC’ magasságvonalak M metszéspontja, továbbá a B’C’ szakasz K középpontja.
8. Adott egy kör és kerületén a P pont. Szerkesszük meg a P-n áthaladó érintőt csak vonalzóval, ha (a) a kör középpontja ismert; (b) nem ismert.
Olimpiai szakkör 2017. január 27. Ezt a szakkört Kiss Viktor tartotta.
1. Egy kör mentén n>3
kártyát helyeztünk el úgy, hogy mindegyik kártyának a hátoldala látható. Egy
lépésben három szomszédos kártyával az alábbi helycserét végezhetjük: a három
közül az egyik szélső kártyát a másik szélső kártya helyére tesszük, a
fennmaradó két kártyát pedig eggyel odébbtoljuk és
megfordítjuk. Ilyen lépések sorozatával elérhető-e, hogy minden kártya a
kiindulási helyére kerüljön és az előlapja legyen
látható? (Kürschák 2007/1)
2. Két játékos előtt egy-egy kavicskupac található,
kezdetben mindkettőben k kavics van. Először az első játékos ezekhez hozzátesz
összesen 2008 újabb kavicsot, az új kavicsokat tetszőlegesen oszthatja el a két
kupac között (akár az összeset is az egyik kupacba
teheti). Ezután a második játékos tesz hozzá a kupacokhoz összesen 2008 újabb
kavicsot, és ugyanígy folytatják felváltva. Az nyer, akinek a kupacában (a
saját vagy ellenfele lépése után) a kavicsok száma négyzetszám, míg ellenfele
kupacára ez nem igaz (ha mindkét kupac ilyen, akkor a játékot folytatják).
Van-e végtelen sok k-ra a második játékosnak nyerő stratégiája? (OKTV
2007/2008/2)
3. Legyenek n és k pozitív egészek, amelyekre k > n és k − n páros szám. Adott 2n
lámpa, amelyek 1-től 2n-ig vannak
számozva, és amelyek mindegyike be(kapcsolt) vagy ki (kapcsolt) állapotban
lehet. Kezdetben mindegyik lámpa ki állapotban van. Lépések egy sorozatát
tekintjük: egy lépés abból áll, hogy valamelyik lámpa állapotát megváltoztatjuk
(be-ről ki-re vagy ki-ről
be-re). Legyen N az olyan, k lépésből álló sorozatok száma, amelyek
eredményeképpen az 1-től n-ig számozott lámpák bekapcsolt, az (n + 1)-től 2n-ig számozott lámpák pedig kikapcsolt állapotban
lesznek. Legyen M az olyan, k lépésből álló sorozatok száma, amelyek
eredményeképpen az 1-től n-ig számozott lámpák bekapcsolt, az (n + 1)-től 2n-ig számozott lámpák pedig kikapcsolt állapotban
lesznek, és a sorozatban az (n+1)-től 2n-ig számozott
lámpák semelyikét sem kapcsoljuk be semmikor. Határozzuk meg az N/M hányados
értékét. (IMO 2008/5)
4. 2x1-es dominókból tornyot építünk a következő módon.
Először elrendezünk 55 dominót úgy, hogy egy 10x11-es téglalapot fedjenek le;
ez lesz a torony első szintje. Erre azután további, 55 dominót tartalmazó
szinteket építünk, ügyelve arra, hogy minden egyes szint pontosan illeszkedjék
az előzőre. Az így kapott építményt akkor nevezzük stabilnak, ha a 10x11-es
téglalap minden rácsponttól különböző, belső pontja felett van dominónak belső
pontja. Hány szintből áll a legalacsonyabb stabil torony? (Kürschák
2005/3)
5. In a mathematical
competition some competitors are friends. Friendship is always mutual. Call a group of competitors a clique if each two
of them are friends. (In particular,
any group of fewer than two
competitors is a clique.)
The number of members of a clique is called its size. Given
that, in this competition, the largest size
of a clique is even, prove that the
competitors can be arranged in two
rooms such that the largest
size of a clique contained in one
room is the same as the
largest size of a clique contained in the other
room. (IMO 2007/3)
Olimpiai szakkör 2017.
február 10.
1.
![]()
2.
Legyen N olyan 16 jegyű poz.eg., amelynek jegyei között a 0, 1, 4, 9 nem fordul elő. Biz, N-nek van néhány olyan egymást követő
jegye, melyek szorzata négyzetszám. Igaz-e ez 15-re is?
3.
Egy ABC háromszög súlyvonalaiból
szerkesztett háromszög hasonló az ABC-hez. Biz. a háromszögnek legfeljebb egy szöge lehet
π/3-nál nagyobb.
4.
Van n változónk a [0;6]
intervallumból, melyekre ![]() . maxP=?
. maxP=?
5.
Egy egységnyi
befogójú egyenlőszárú derékszögű háromszöglemez valamennyi pontját kiszínezzük
négy szín valamelyikével. Bizonyítsuk be, hogy bármely színezés esetén van két
olyan azonos színű pont, amelyek távolsága legalább ![]() .
.
6.
Biz. az n!+1, …, n!+n mindegyikének van olyan prímosztója, mely a
többi n–1 egyikének sem osztója.
7.
Az ABC háromszög oldalait a beírt kör A’, B’,
C’-ben
érinti. Legyen M a beírt kör
tetszőleges pontja. Igazoljuk, hogy M-nek
az ABC oldal-egyeneseitől mért
távolságainak szorzata ugyanakkora, mint amekkora ez a szorzat az A’B’C’ háromszög esetén.
8.
Három hajótörött
mindegyike egy-egy órát tölt (egyhuzamban) egy szigeten délután 5 és 9 óra között
véletlenszerűen. Ha hármuk közül pontosan kettő fél óránál hosszabb ideig
egyszerre tartózkodik ott, akkor viszály tör ki. Mekkora a valószínűsége, hogy
békében telik el a nap?
Olimpiai szakkör 2017.
február 24.
1. A nemnegatív egészeken értelmezett
t(n) fvényre t(0)=t(1)=0,
t(2)=1. Ha n>2, akkor t(n) a legkisebb olyan poz. eg., amely nem osztja az n
számot. Legyen T(n) =t(t(t(n))).
Határozzuk meg S=T(1)+T(2)+…+T(2006) értékét.
2. Adott a síkon egy K középpontú egységsugarú kör és egy ezt
nem metsző e egyenes. K-ból az e
egyenesre emelt merőleges talppontja O, KO=2. Legyen H azoknak a köröknek a
halmaza, amelyeknek a középpontja e-n van és kívülről
érintik a K középpontú egységkört. Biz. van a síkon olyan P pont, amelyből H
minden körének e-n levő átmérője ugyanakkora (0-nál nagyobb) szögben látszik.
Határozzuk meg P helyzetét és a látószög mértékét.
3. Az r és s pozitív egészekről tudjuk, hogy bármely k pozitív
egészre ks-nek legalább annyi osztója van, mint kr-nek. Lássuk be, hogy r osztója s-nek.
4. Egy kocka élhossza n egység. A
felületét alkotó egységnégyzetek közül max hányat
jelölhetünk ki úgy, hogy semelyik kettőnek ne legyen közös oldala?
5. Melyek azok az (a;b;c) rendezett
valós számhármasok, amelyekre bármely változót kivonva a másik kettő
szorzatából 2007-et kapunk?
6. egy négyzetet oldalaival párhuzamos
egyenesekkel 16 négyzetre bontunk. Ezeket pirosra vagy kékre színezhetjük,
bármely 2×2 vagy 3×3 –asban a négyzetek színét az
ellenkező színre változtathatjuk. Kezdetben minden négyzet piros. (a)
elérhető-e, hogy a felső sor második négyzete kék, a többi piros legyen? (b)
Biz legfeljebb 212 féle színezés lehetséges.
7. Biz. bármely háromszöghöz található olyan e
egyenes, hogy H-nak az e-re vonatkozó tükörképe H területének több, mint
¾ részét fedi.
8. Jelölje p(i) az i-dik
prímet és legyen Q(k)=p(1)p(2)…p(k). pl Q(4)=210. Biz
az 1, 2, …, Q(k) számok között pontosan Q(k)/2 darab
olyan van, amely a p(1),…,p(k) közül páratlan sokkal osztható.
Olimpiai szakkör 2017. március 10.1. A pozitív egész k szám jegyeinek összege legyen S(k). Határozzuk meg az összes olyan egész együtthatós P(x) polinomot, amelyre minden n>2017 esetén P(n)>0 és S(P(n))=P(S(n)). 2. Adott a síkon 2n+1 különböző egyenes, nincs köztük egymásra merőleges. Legfeljebb hány hegyesszögű lehet az egyenesek által meghatározott háromszögek közt?
3. Határozzuk meg azon n poz. egészeket, amelyeknek összes poz. osztója elrendezhető egy téglalap alakú táblázatban úgy, hogy (i) a táblázat minden mezőjébe különböző osztó kerül; (ii) minden sorban ugyanannyi a számok összege; (iii) minden oszlopban ugyanannyi a számok összege.4. Az a1,a2,…sorozatban a1=c poz. eg., továbbá. Biz. " elem poz. eg.
5. Az ABC
háromszögben AB=AC≠BC, jelölje a
beírt kör középpontját I. A BI egyenes AC-t D-ben metszi. A D-n
áthaladó AC-re
merőleges egyenes AI-t
E-ben metszi. Igazoljuk, hogy I tükörképe az AC egyenesre rajta van a BDE
háromszög köré írt körön.
6. Egy feleletválasztós
tesztvizsga 4 kérdésből állt. Minden kérdésre háromféle válasz volt adható. A
vizsgán résztvevő diákokról kiderült, hogy bármely hármójukhoz volt olyan
kérdés, amelyre mindhárman másképpen válaszoltak. Legfeljebb hány diák vehetett
részt a vizsgán?
7. Határozzuk meg azokat az f:Q®Q függvényeket, amelyekre teljesül, hogy bármely két x,y racionális számra f(x+y)=f(x)f(y)–f(xy)+1.
Olimpiai szakkör 2017. március 24.1. Legyen H={1,2,...,n}. Megadható-e két, közös elem nélküli A és B halmaz, melyek uniója éppen H úgy, hogy A elemeinek összege egyenlő B elemeinek szorzatával, ha (a) n=2016; (b) n=2017? 2. Bizonyítsuk be, vagy cáfoljuk meg a következő állítást: minden pozitív egész k számhoz létezik olyan n szám, hogy azbinomiális együttható osztható k-val minden 0<i<n esetén.
3. Az ABC háromszög A-ból induló magasságának talppontja T, a B-ből induló szögfelező az AC oldalt D-ben metszi. Tudjuk, hogy BDAÐ=45°. Mekkora a DTCÐ?
4. Tekintsük az n-dik Csebisev polinomot, melyre Tn (cosx)=cosnx minden x-re. Mi a főegyüttható? Mennyi az együtthatók összege? Mit mondhatunk a zérushelyekről? 5. (a) Igazoljuk, hogy n különbözőalakú (de nem feltétlen különböző értékű) racionális számot kiválasztva a (0; 1) intervallumból, a számok nevezőinek összege legalább
(b) Igazoljuk, hogy ha feltesszük a számokról, hogy különböző értékűek is, akkor a számok nevezőinek összege legalább.
6. Legyenminden olyan x,y,z-re, amelyre x+y+z≠0. Keressünk olyan a,b,c-t, amelyre
és 1,999<f(a,b,c)<2.